Experimenting with rendering in Fourier space

Constant magnitude, drawing sine waves into phase space, then running inverse DFT to generate image:

Okay so I've been doing a bunch of experiments with 2D Fourier transforms at @LevelExGameDev for the past few days; gonna make a thread to document this stuff so I don't forget it lol

So here we have the Space Sloth, and its accompanying Fourier-space representation

Fourier transform results in a complex number, so it's easiest to represent in polar coordinates. Phase is displayed on the top left, magnitude below

Not gonna do a full explanation of how to understand the Fourier images; they're not entirely human-readable except for a few specific properties

If you want to read up on it, best explanation I've found is here:

Main takeaways:
- You can convert freely between real and Fourier representations without losing information

- Fourier space represents the image as a huge collection of cosine waves all added together. Waves can be described as frequency, amplitude, and phase offset

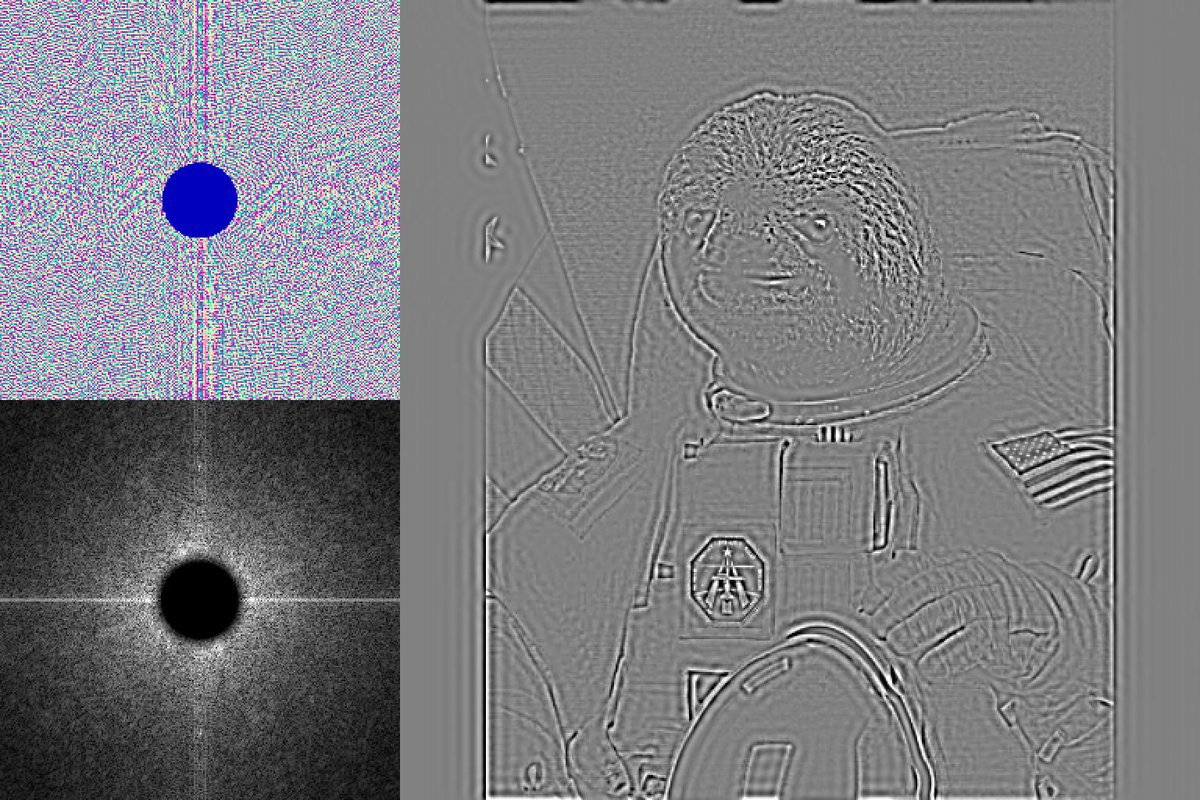
Every pixel coordinate in the Fourier image corresponds to a FREQUENCY, not a LOCATION. Amplitude and phase of the waves are related to the magnitude and phase values in the Fourier images

Lower frequencies are towards the center, but beyond that the pixel coordinates in Fourier space have NO positional relationship to the pixels in the real image

Thus, things like blurring or warping the Fourier image mostly result in uninteresting garbage, sadly

So, basic idea for these experiments:

Convert image to Fourier space via Discrete Fourier Transform, edit the frequencies, then convert back to real image via Inverse Discrete Fourier Transform

Here's Guassian(ish) blur:

Literally just throwing out the high frequencies (i.e. sharp changes in brightness over small pixel distances) and keeping the low frequencies (big, smooth changes in brightness over large distances)

If you're familiar with audio this would be a low-pass filter

Turns out Guassian blur is literally a 2D low-pass filter. Audio is a 1D signal and images are 2D signals, but the math's the same

A huge amount of Photoshop is basically digital signal processing tools

Good note here

(I'm prob gonna get some things wrong here; DSP is very much not my area of expertise, which is why I was interested in messing around with it)

Opposite of low-pass filter is high-pass, obv

(The actual values here go negative, so I've remapped it for display, which results in 0 being 50% gray)

Axes through Fourier space correspond to angles in real space, thus you can do oriented effects like a directional blur pretty easily:

Bandpass filters at different frequency ranges look very cool

Everything I've shown so far is just multiplying the DFT with different masks

Multiplication in Fourier space is equivalent to convolution in real space (!), which is a HUGE topic that I'm not really equipped to discuss

but basically you can do all this with kernels if you want

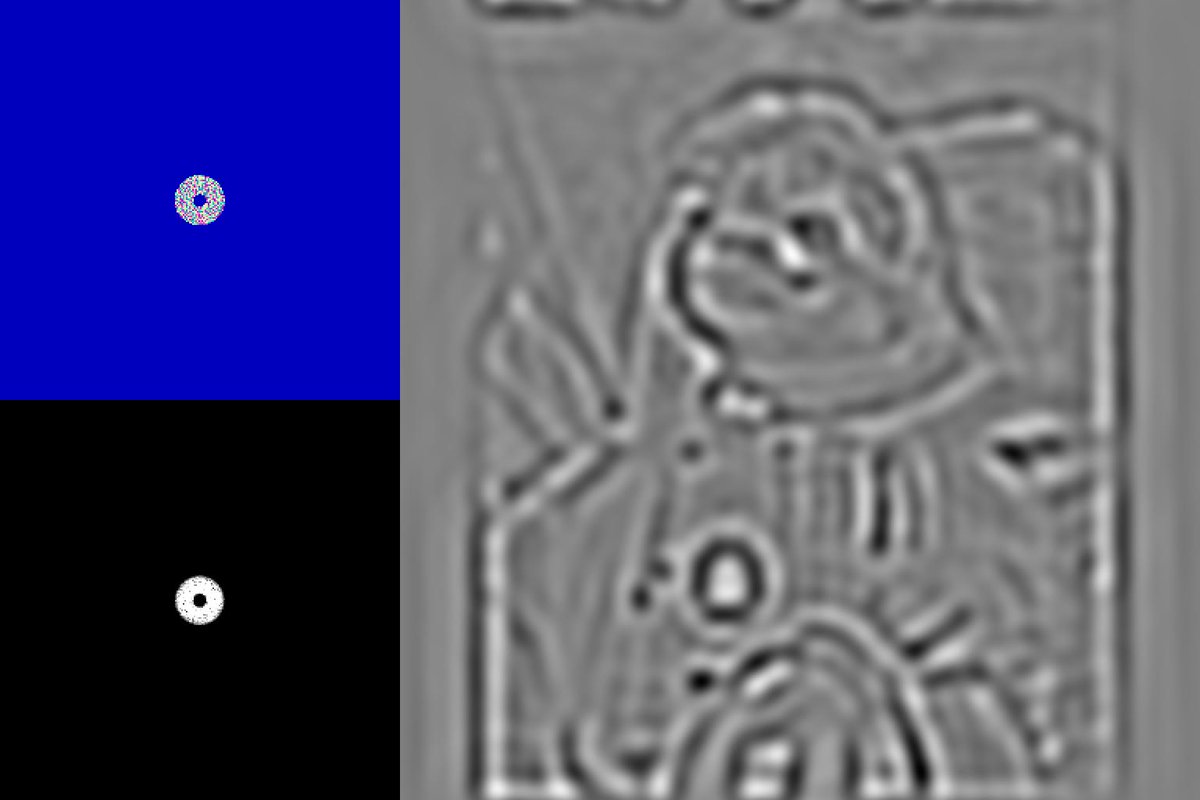
Things get WAY more interesting when you start screwing with the magnitude and phase values independently; you can start getting some really wild effects that don't transfer readily to any other screenspace technique

Here's the result of keeping the frequency distribution unchanged but writing random angles into the phase offsets

Our friend the sloth is completely gone but you can still see strong vertical components from the black bars in the original image

Leaving the phases alone and writing random magnitudes for the different frequencies, interestingly, still results in a recognizable image

The phase offsets create destructive and constructive interference across the whole image, so this is *somewhat* intuitive. Any individual oscillation (i.e. one pixel in the DFT) isn't going to contribute much to the overall image, unless its phase aligns with LOTS of other waves

...This is a bit demoralizing if you want to generate cool images though, bc the phase offsets are INCREDIBLY unintuitive to work with. Remember, they have no particular spatial relationship, they're just describing interference patterns between 512x512 different waves

drawing procedural shapes into phase space proved extremely difficult as a result. Can't really intuit what anything's going to do, so I was just trying stuff at random. Concentric waves, as shown at the start of this thread, look very neat though

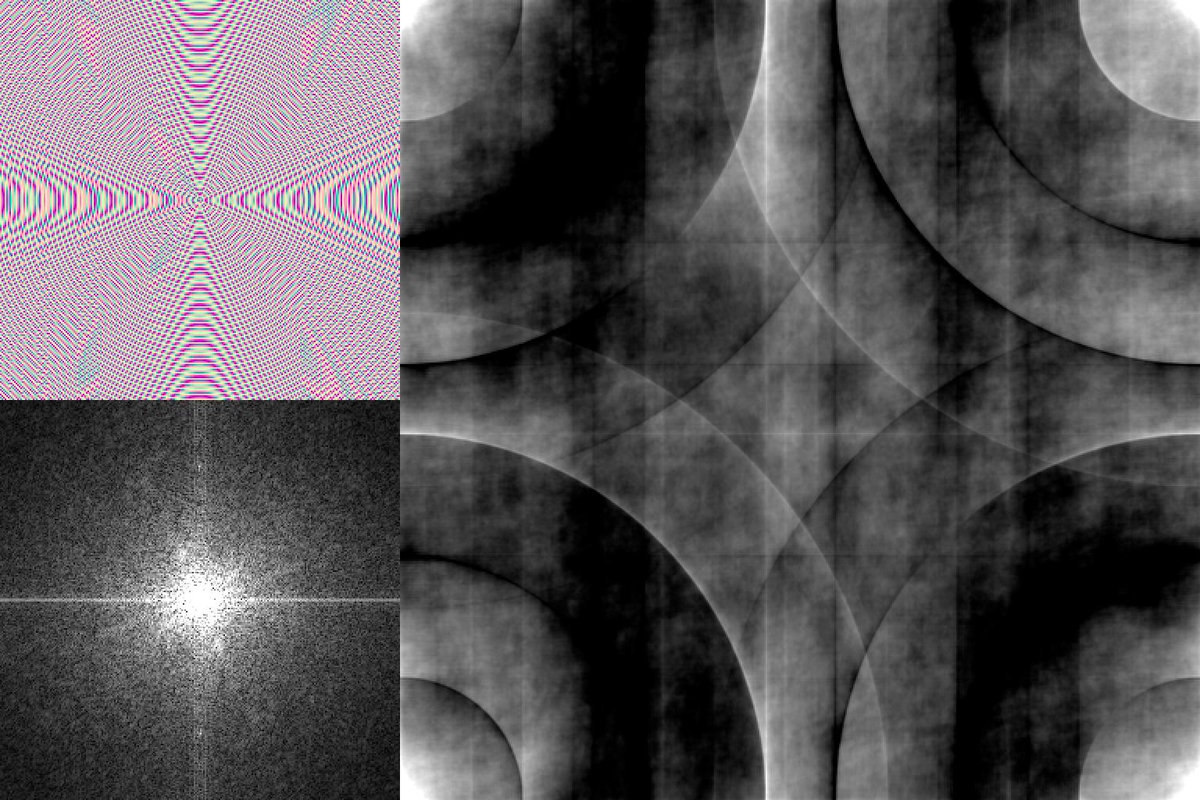
Drawing procedural stuff into the magnitudes though?

HYPNOSLOTH

(twitter compression will probably ruin this sorry)

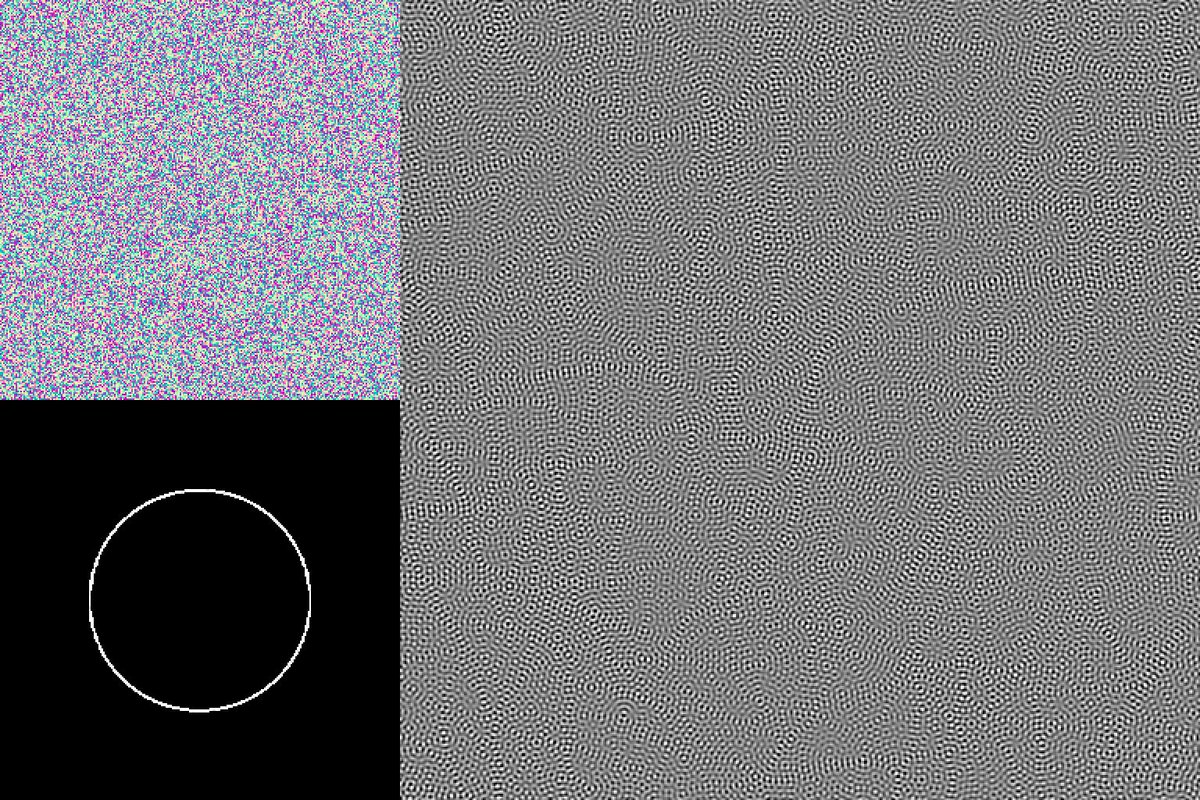
One REALLY neat application for all of this is noise generation. Recall that noise is often classified by its frequency distribution ("white noise" etc)

Noise is basically random waves in specific frequency ranges, which means you can construct pretty much any noise you want by drawing the appropriate frequency distribution and then just using random phases

- White noise (all frequencies equally)

- Blue(ish) noise (higher freq only)

- Simplex(ish) noise (Low only, sharply delineated)

- fBm (all frequencies, with higher freqs falling off exponentially)

You can also animate all of these trivially by just rotating the phases (and you can get some subtle effects by animating different frequency ranges at different speeds), and anything you make will tile just by nature of how DFT works

Really narrow-band noises are extremely weird and cool (if these have a name I don't know what it is)

You can also get some really pleasing textures by drawing various procedural shapes into the frequency distribution

Lots of room left to explore here but unfortunately I need to stop in order to get actual work done lol

Anyway, none of this is particularly novel; the analog version of this stuff predates computers, and Fourier transforms (and/or the related discrete cosine transform) are a huge part of image and video compression

I just don't see it talked about a whole lot in tech-art spaces

The biggest downside is it's slow as hell. Naive DFT is separable but every fragment has to sample every other texel in its row+column, so if you're doing DFT->manipulate->Inverse DFT that's 4N samples per fragment

the "Fast" Fourier transform you've probably heard of is log(n), which rules, but it's a recursive algo that doesn't intuitively map to a parallel GPU approach

I'm sure someone much smarter than me has prob figured it out though

Also, credit: my DFT implementation was largely derived from @FabriceNEYRET 's work:

Go check out the rest of their shadertoy stuff; it's fantastic